Exercícios Resolvidos

1º)(FFT) Considere a Terra como uma esfera de raio 6.370km. Qual é sua área superficial? Descobrir a
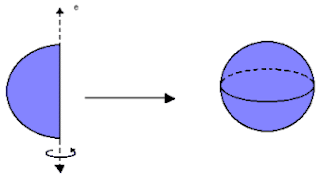
área da superfície coberta de água, sabendo que ela corresponde a aproximadamente 3/4 da superfície
total. Resp. → Aa ≈ 382.234.398 km2.

Solução:

At = 4π x r2 ≈ 4 x 3,14 x 6.3702. Portanto, At ≈ 509.645.864km2. A

superfície coberta por águas é dada por Aa = 3/4 x 509.645.864.

Logo, Aa ≈ 382.234.398km2.

2°)Uma laranja tem a forma de uma esfera, cujo diâmetro mede 8cm. Então a área aproximada da casca dessa laranja é:
a) 190cm2.
b) 200cm2.
c) 210cm2.
d) 220cm2.
e) 230cm2.



3°) Considere uma laranja como uma esfera composta de 12 gomos exatamente iguais. Se a laranja tem 8cm de diâmetro, qual é o volume aproximado de cada gomo?
a) 19cm3.
b) 20cm3.
c) 21cm3.
d) 22cm3.
e) 23cm3.




4°)(UFRGS) São fundidas 300 esferas com 20mm de diâmetro para fabricar cilindros circulares retos com 20mm de diâmetro e 200mm de altura. O número de cilindros resultantes é:

a) 2.
b) 5.
c) 20.
d) 25.
e) 30.

5°)(CEFET-PR) A indústria de bolas de borracha Cilimbola quer produzir embalagens cilíndricas para colocar 3 bolas com 3cm de raio cada, conforme a figura. A quantidade total de material utilizado para o fabrico da embalagem, incluindo a tampa, em

cm2, será de:
a) 126 p b) 108 p


b) 108 p
c) 127 p d) 72 p
d) 72 p
e) 90 p

GABARITO


1 B
2 D
3 C
4 A
5 B

Nos Bastidores *------*

Geometria Espacial - Esfera.

Esfera

Chamamos  esfera de centro O e raio R o conjunto de pontos do espaço cuja distância ao centro é menor ou igual ao raio R.

Considerando a rotação completa de um semicírculo em torno de um eixo e, a esfera é o sólido gerado por essa rotação. Assim, ela é limitada por uma superfície esférica e formada por todos os pontos pertencentes a essa superfície e ao seu interior.

Esfera é o conjunto de pontos do espaço cuja distância a O é igual ou menor que o raio R.

Área da superfície esférica e volume da esfera




A área da superfície esférica de raio R é dada por:
                       
O volume da esfera de raio R é dado por:
                   

 Superfície esférica

A superfície esférica de centro O e raio R é o conjunto de pontos do es[aço cuja distância ao ponto O é igual ao raio R.

Se considerarmos a rotação completa de uma semicircunferência em torno de seu diâmetro, a superfície esférica é o resultado dessa rotação.

  A área da superfície esférica é dada por:

Secção de uma esfera

OO’ é a distância do plano α ao centro da esfera. Qualquer plano α que seciona uma esfera de raio R determina como seção plana um círculo de raio R.

Sendo OO’ = d, temos:

Quando o plano que secciona a esfera contiver um diâmetro, teremos d = 0. Nesse caso, o círculo determinado terá raio R e será denominado círculo máximo.